
立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
柱と錐の体積 どちらも公式は簡単です。 柱の体積=底面の面積×高さ 錐の体積=底面の面積×高さ÷3 錐の高さは、頂点から底面に垂直に引いた線です。真っ直ぐの線です。斜めの線ではないので気をつ体積の求め方について、自分の捉え方やイメージについて、 ペアや班で伝え合う。 3 角柱、円柱の体積の求め方を活用する。 角柱や円柱などの立体の体積を求める問題に ついて、ペアや集団で考えを伝え合う。 複数の立体を示し、公式を使用して体積を求
立体の体積の求め方 公式
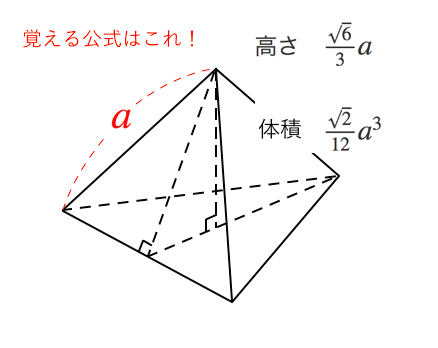
立体の体積の求め方 公式-くさび形の体積 非常に参考になりました。 ちなみにa<cでもこの公式は成り立つのでしょうか? 他の会社員・公務員の方で「盛土計算」でこの式を利用されている方がいますが、「盛土計算」では使用しないでください。 基本的に平均断面法による体積四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 体積の求め方、覚え方 体積の公式の覚え方は簡単です。球の体積を除けば、たった2つの公式を覚えるだけで済むからです。

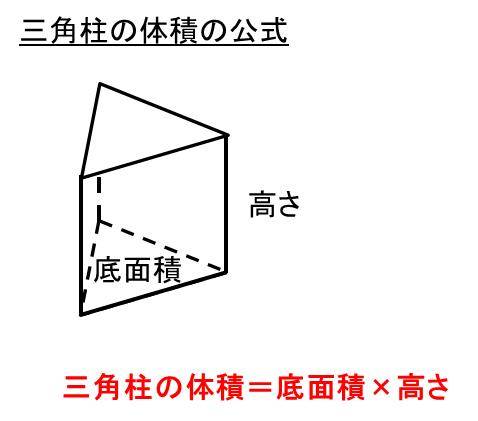
三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学
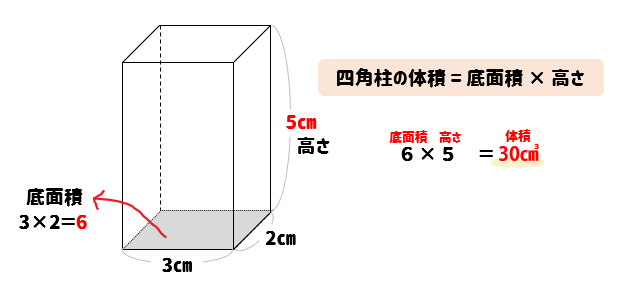
立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm6年算数 立体の体積 角柱と円柱の体積 学習支援 by いっちに算数 スマホ版 立方体 直方体 6年生は、上の図のように5年生で勉強した「直方体や立方体」の体積の求め方を生かして、下の図のような「三角柱などの角柱や円柱」の体積の求め方を勉強します。 角柱の体積を求める問題です。 公式自体は難しいのもではないので、図形を見て底面積がどこかをしっかり確認してください。 5年生の角柱の基本事項も復習しておきましょう。 角柱の体積は 底面積×高さ で求めることができます。角柱は底面が三角形なら三角柱、四角形なら四角柱、五
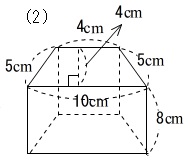
楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り2章 空間図形 48 140 次の図の立体の体積を求めよ。 ⑴ ⑵ 138 次の図の角錐の体積を 求 めよ 。 ⑴ ⑵ ⑶ 141 右の図のよ う に ,1 辺 12 cm の立方体から,3 点 A ,C ,F を通る平 面で切ってできる 2 つの立体のうち,小さい方の立体を取り除いた。立方体の公式と計算(求め方) 立方体の公式を下記に示します。 立方体の体積=a 3 aは1辺の長さです。その他の立体図形の体積の算定は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積
立体の体積の求め方 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1 |  1 |  1 |
 1 | 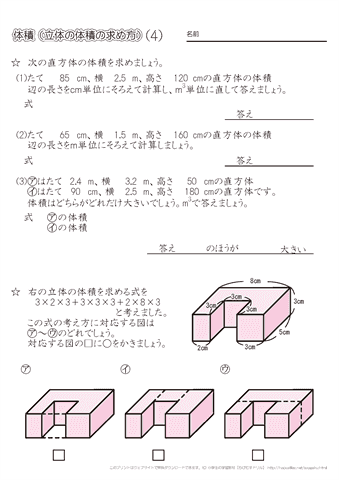 1 |  1 |
 1 | 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 1 |
 1 |  1 |  1 |
 1 | 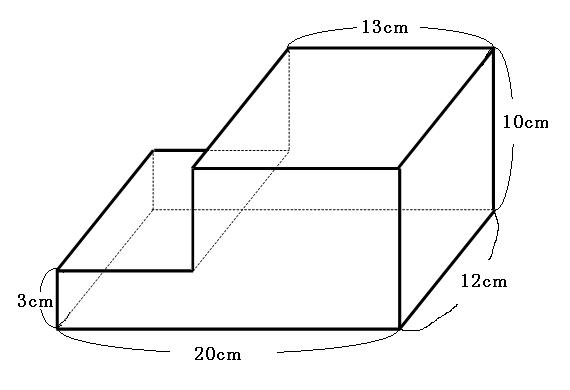 1 |  1 |
 1 |  1 | 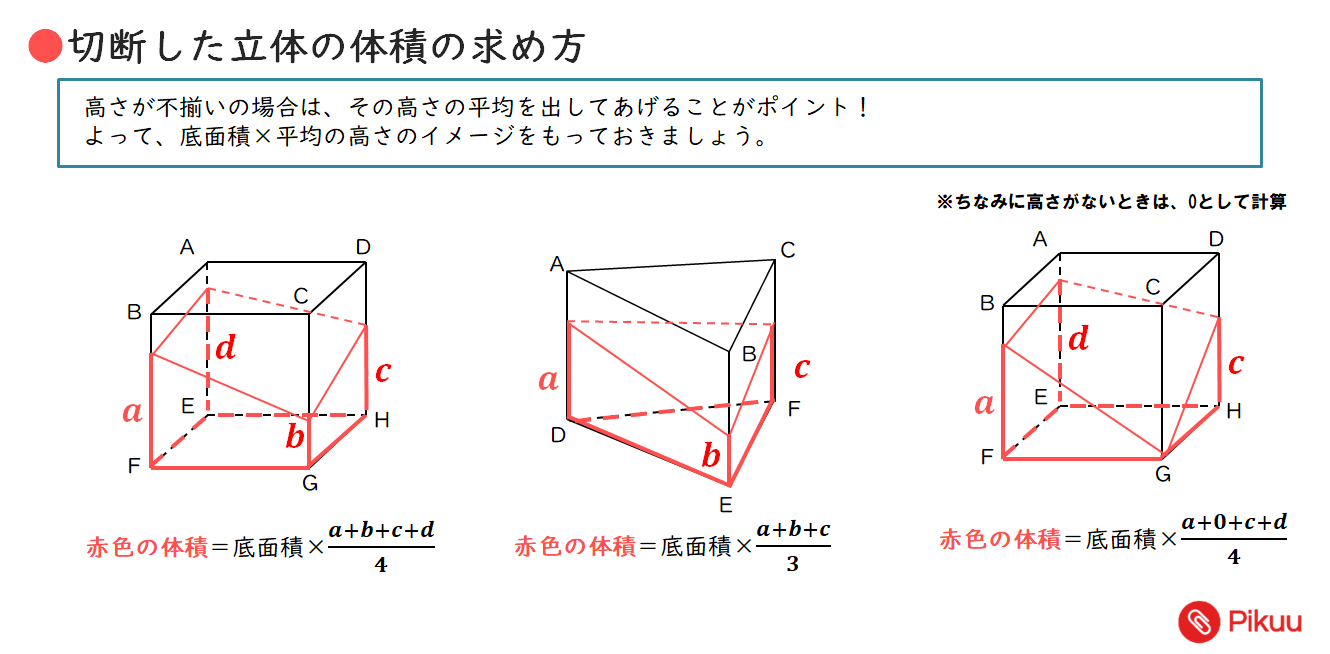 1 |
 1 |  1 |  1 |
 1 | 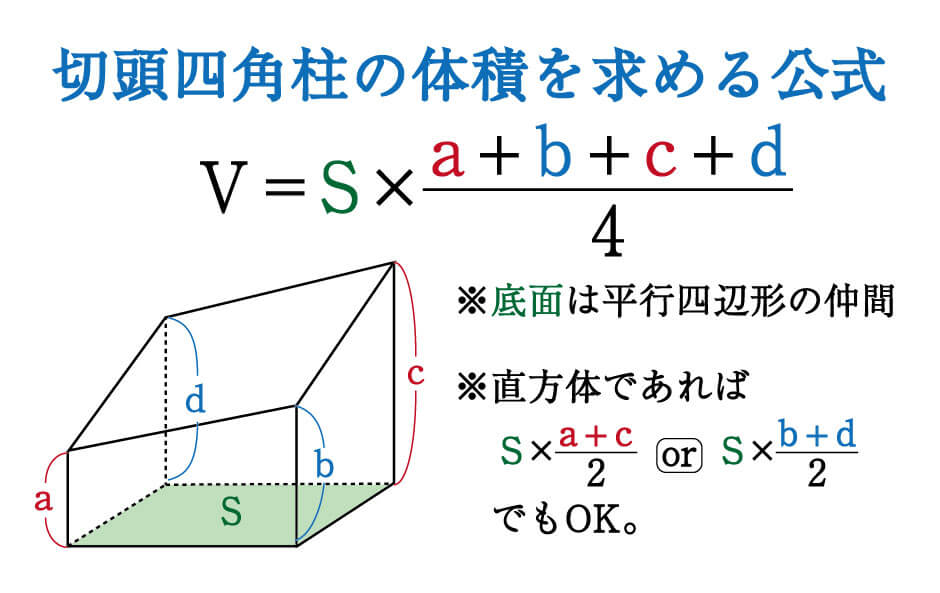 1 |  1 |
 1 | 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 | 1 | 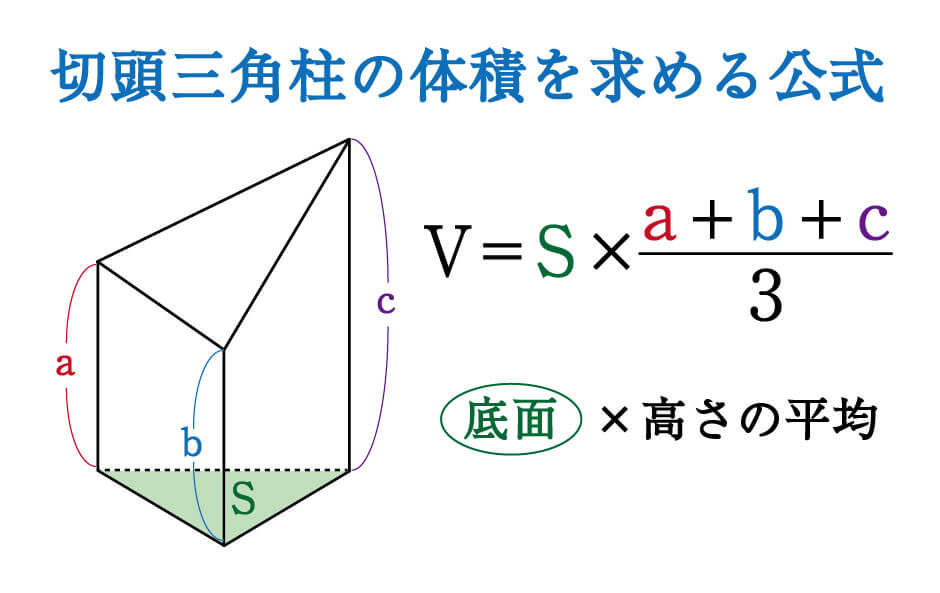 1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
1 | 1 |  1 |
1 |  1 |  1 |
 1 |  1 |  1 |
1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
1 |  1 | 1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 1 |
 1 |  1 |  1 |
 1 |  1 |
球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。 球 最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。
Incoming Term: 立体の体積の求め方 公式,



